- A+
王者荣耀电竞竞猜就来蜗牛电竞——(www.allnew366.com)
蜗牛扑克allnew官网,蜗牛扑克allnewpoker官网,蜗牛扑克allnewpoker国际场,allnewpoker官网下载,蜗牛扑克网站,蜗牛扑克下载——(allnewpuke.com)
剪刀石头布
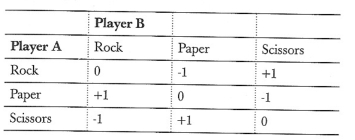
第二个,稍微复杂点用来诠释同样概念的游戏是剪刀石头布。在这个游戏里,玩家从3个选项中做出选择,并获得如下收益表:
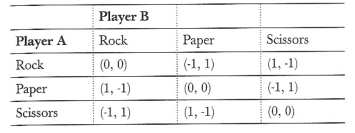
通常,本书中提及的游戏都是零和游戏,如果有非零和的都会详细标注出。下面的表和上面的等价,除了是以A的角度出发:
如果B想确保0期望,他可以使用{1/3,1/3,1/3}的策略。用类似计算奇数偶数游戏的方法,(可以得知)无论A选择出什么,他都会在1/3的时候赢1个单位,在1/3的时候打平,在1/3的时候输1个单位。任何其他B的选择都会导致强敌通过用一个单纯策略对抗进行剥削。所以这是该游戏的一个最优策略。
在这类游戏会经常发生的一个情况是,强敌有2个或者跟多剥削策略可以使用。B选择了他的策略,而强敌选择剥削策略回应。当B选择了某个策略S的时候,强敌的剥削策略会不偏不倚:意思是说,无论选择哪个策略都不会改变期望值。这个不偏不倚的阈值就是B的最优策略。这个概念如此重要的原因是,可以让我们确保找到的策略不能通过在任何方向有一点点的改变来改善。无比记住,一个策略最优的条件之一是,任何一个玩家都不能通过单边改变策略来改善。当一个玩家在选择策略不偏不倚时,这也保证了这个条件不被打破。
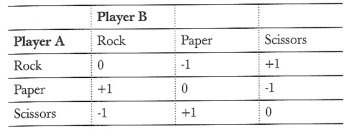
为了让我们更简单地找出最优策略,我们来看看一个调整过的剪刀石头布,当用剪刀获胜时,有额外奖励。我们叫他剪刀石头布S,收益表如下:

现在{1/3,1/3,1/3}的策略很容易被对手{0,0,1}(即只出剪刀)而打败,并且对手总共可以赢1/3个单位。然而,A可以降低游戏的期望到0通过努力让对手的选择不偏不倚。
假设A的策略是{a,b,c}。那么那么A希望让B不同策略的期望相等,使用公式1.11:
< B,石头 > = 0 × a + (-1) × b + (1) × c
< B,石头 > = c – b
< B,纸 > = 1 × a + (0) × b + (-2) × c
< B,纸 > = a – 2c
< B,剪刀 > = (-1) × a + 2 × b + (0) × c
< B,剪刀 > = 2b – a
令这3个数值相等,我们可以得到a = 2b = 2c也就是说,策略将会是{1/2,1/4,1/4}.我们可以间接地验证这是个最优策略。首先,这个游戏是对称的,所以任何B使用的策略,A也可以使用。因为收益之和为零,所以没有策略可以在面对强敌时期望大于零。如果这种策略存在,那么当两个玩家都使用这个策略时,将违背零和游戏的本质。所以这个策略一定是最优的。
注意到,对剪刀胜利时增加的奖励促使最优策略更少地出剪刀。我们会经常发现许多情况下有类似这样的防守策略。当规则改变,并且倾向某一种特定的行动时,最优策略通常偏向反抗这个行动的策略而非利用之。我们在扑克中也会有同样发现,一个明显的例子就是,底池越大,我们咋呼越少,因为一次成功的咋呼会更有利可图。
在我们所有讨论过的例子里,所有策略的选项都有同样的“重要性”。每种都代表了策略或者应对策略中一个关键的部分,而且没有策略是因为太弱小而不被使用。然而,实际并非如此;经常会发生的是,在更复杂的游戏里,一种策略S被称为“被主导”,如果策略S’在面对所有对手的策略时,期望都大于等于S,并且至少有一种对手策略,满足S’的期望高于S的期望。此时,我们称S’主导了S。
这个应该非常好理解;如果我们有一个策略可选,而有其他策略在应对对手所有策略上至少打平,有时更好,我们应该总是选择那个更好的策略。我们来看一下另一个版本的剪刀石头布。这次,我们不改变收益表,而是引入一个新的选择,“花”。花会输给所有的石头和剪刀,跟纸或者花打平。

很显然,没有任何包含花的策略会比把花换成纸更好。因此,花被纸主导了。我们也有了第二个术语,严格主导,意味着策略S’在应对所有策略时,都比S表现更好(没有相等)。这通常发生在没有选择的情况下;扑克中的一个例子就是当对手在现金桌翻前全下时,你是最后一个玩家并且手握AA。无论对手的策略是什么,你跟注的期望都高于弃牌。因此,跟注严格主导弃牌。很显然,最优策略不能包含被严格主导的选项;因为如果有,那么玩家可以简单地用更好期望的选择进行替换来单方面提升。
策略选择通常都很有价值;实际上,我们目前而言所有的零和二人游戏里,策略选项都有非负值。增加一个额外的策略选择,不会降低玩家在游戏里的期望,因为他可以假装没有这个新选择,而用旧的策略保持之前的期望。然而,通常他可以把新的选择融合进自己的策略里提高收益。
另一个我们经常会用来描述策略的词是含优。有时最优策略组合中包含许多策略,在某些情况下包含一些被主导的策略。这也许会让某些读者吃惊,但是一个例子应该可以说明问题。加入剪刀石头布F(带花的版本),我们加入一个策略选项:“安全剪刀”,它会一样赢纸,输给石头,但是还会输给花。所以这个版本里,出安全剪刀一定被出剪刀所主导。然而,包含安全剪刀的策略依然可以是含优的,因为他们可以是最优策略的一部分。这是因为最优策略永远不包含花,因此,安全剪刀和普通剪刀是一样的。
当我们在扑克中探索最优策略,然而,我们主要考虑寻找不被主导的策略,因为从对手的失误中获得价值非常重要而且相当频繁。
当有被主导的策略选项存在时,我们可以用一个循环的方式来简化游戏。在上面的例子里,我们从一个完整的收益表开始:
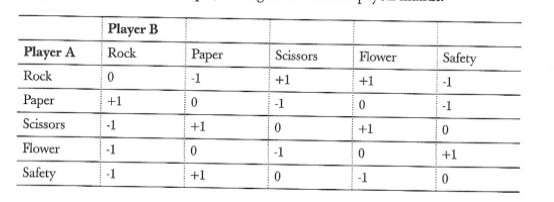
我们可以通过比较“安全剪刀”和“剪刀”的收益值发现前者是一个被后者主导的策略。在所有情况下,“剪刀”的收益始终大于或者等于“安全剪刀”。因此,“安全剪刀”是被“剪刀”主导的。当我们寻求最优策略时,我们可以把这个游戏简化到没有一个玩家会出“安全剪刀”的版本:
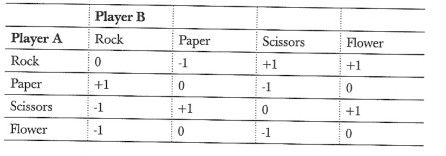
于是这个游戏变成了我们之前提到的剪刀石头布F(带花的版本)。重复之前的过程,由于花也是一个被主导的策略可以被移除:
我们就回到了最基本的剪刀石头布。因此,这个包含了“花”和“安全剪刀”的扩展版剪刀石头布的策略和最初的版本其实一致。这个循环的过程可以用来简化许多游戏。通常这会非常有用,因为它可以减少许多必须考虑策略选项,总而言之:
一个游戏G可以通过移除双方被主导的策略选项而简化成子游戏G’。此时G’的最优策略也是G的最优策略。
好消息 蜗牛扑克GG扑克室-全新德扑玩法“极速&现金桌"上线!
全天24小时随机将掉落现金红包至牌局底池或玩家余额!快体验吧
蜗牛扑克优惠提供30%超高额返水
蜗牛扑克官方网址:www.allnew366.com
蜗牛扑克网址发布页:www.allnewpuke.com
蜗牛娱乐官网:www.allnewbet8.com
蜗牛扑克GG官网:www.ggallnew.com











